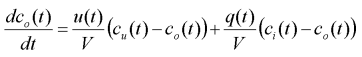|
You are here : Control System Design - Index | Simulations | pH Simulation | Part 2 pH Control - Part 2Flow VariationsIf the system's influent flow is from some sort of industrial runoff, then it is highly likely that the flow rate will vary, since the runoff will not be at a constant rate. The variation in influent flow rate presents itself as an input disturbance in the plant model.
where q(t) is the flow rate signal. In this example, we model the fluctuations as a constant flow plus some randomly varying noise. In particular, we set the average flow to the level used in the last example (10 L/min), and the random variations range uniformly between -1 L/min and 1L/min. We will use the same controller as in the last example, which is based on the nominal flow rate of 10 L/min. However, we should note that allowing the q(t) input to vary with time makes the system more non-linear than before. Java Applet SimulationBelow is a Java applet which simulates the pH control system with influent flow rate variations. The blue plot shows the influent concentration and the green plot shows the effluent concentration. This process is extremely slow, so the time scale is accelerated somewhat: 1250 simulated seconds pass for each real second of the simulation, giving a horizontal scale of 2500 seconds per division Pressing the "Change Parameters" button brings up the parameters window allowing you to change the controller values, the influent pH and the animation speed. The controller has been implemented in the anti-windup form to avoid the effects of the saturation of the valve. The animation speed can be 25, 12.5 or 6.25 frames per second. This speed is only the rate at which the screen is refreshed - the simulation is unaffected. The speed function is available for those with slower computers so that the simulations still appear in real-time (if somewhat jerkier). Note that the applet does some auto-detection of the speed of your computer, so if you select a speed that your computer cannot handle, the applet will reduce the speed accordingly.
The output variations occur because of the relative size of the tank and the influent valve. If this valve is larger, the influent flow rate increases, and liquid flows through the entire system at a faster rate. This means that the filtering effect of the tank is reduced somewhat. As you might expect, increasing the tank volume would reduce the pH variations in the effluent. However, building a bigger tank is expensive, and as we will see in the next example, errors in the control valve reduce the effect of a bigger tank anyway. |