You are here : Control System Design - Index | Simulations | pH Simulation | Part 4
pH Control - Part 4
Multiple Tanks
To overcome the flow variations and the valve hysteresis problems, we use a 3 tank system where the tanks increase in volume. This setup is shown in the diagram below.
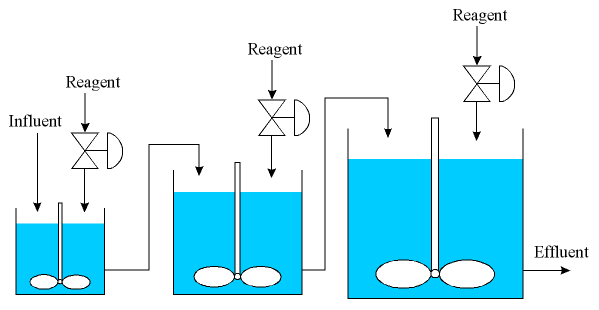
The influent flows into the first tank, which has a large valve to neutralise most of the influent base. The set-point for this control system is set to a pH of 9.6, since the purpose of the 3 tank system is to attack the problem in steps.
The effluent from the first tank flows directly into the second tank, which is 20 times larger. The second tank uses a valve that is 20 times smaller than that used by the first tank. The set-point for this control system is set to pH 8.3.
The effluent from the second tank flows directly into the third tank, which is 20 times larger again. The third tank uses a valve that is 20 times smaller than that used by the second tank (and thus 400 times smaller than the first tank). The set-point for this final tank is a pH of 7.
This scheme takes into account the comparable magnitude of the error sources. The first tank is relatively small, since it requires a large valve to reduce the pH to 9.6. As the liquid flows through the tanks, the variations reduce and the pH gets closer to 7. The final tank performs only minor adjustments, since the second tank has reduced the pH to 8.3. At this final stage, we are able to reduce the valve size and increase the tank volume with no adverse effects.
Having 3 tanks is more expensive than a one tank scheme, but we will see that the 3 tank system is extremely effective. Also, the consideration of the magnitude of the errors ensures that each tank is no larger than it needs to be.
For this simulation, we assume that the first tank has a volume of 83.67 L, and uses a valve which allows a maximum reagent flow rate of 1.5 L / min. Also, the influent flow rate variations are as before with the average flow to the level used in the last example (10 L/min), and the random variations range uniformly between -1 L/min and 1L/min.
Java Applet Simulation
Below is a Java applet which simulates the 3 tank pH control system. The plots shown in the simulation are listed below:
| blue | influent pH |
| green | effluent concentration for the first (smallest) tank |
| red | effluent concentration for the second tank |
| purple | effluent concentration for the third (largest) tank |
This process is extremely slow, so the time scale is accelerated somewhat. There are two speeds at which to view the simulation. The slow speed is the same as that used in the previous simulations, with a horizontal scale of 2500 seconds per division. The fast speed has 10000 simulated seconds passing for each real second of the simulation, giving a horizontal scale of 20000 seconds per division. The plot for the smallest tank loses a lot of information in the fast speed.
Pressing the "Change Parameters" button brings up the parameters window allowing you to change the controller values, the influent pH and the animation speed. The controller has been implemented in the anti-windup form to avoid the effects of the saturation of the valve. The animation speed can be adjusted as before.
Pressing the "Reset" at any time button resets the simulation to its initial state. Also, the "Start/Stop" button allows you to start and stop the simulation at will.
Finally, the pH meter can be attached to any of the tanks in the system by clicking on the appropriate tank in the lower right hand corner of the applet.
| Things to try | Things to notice |
| With the speed set to slow, observe the response of the three tanks | Notice that the effluent pH for the smallest two tanks stays very close to the set point (in steady state) |
| Set the speed to fast | Notice that the effluent pH from the third and largest tank stays very close to 7 (after an initial transient) |
| Change the set-point for the second tank to something larger than 8.3 (such as 9) | Notice that the controller for the third tank can no longer neutralise the base in the influent |
| Change the set-point for all tanks to a pH of 7 | Note that the controller for the second tank cannot neutralise the effect of the widely varying pH in the first tank's effluent |
The three tank system works well when the set-points are uniformly spaced between a pH of 11 and 7. Note that a step of 1.3 in the logarithmic pH scale corresponds approximately to a multiplicative factor of 20 - hence the scaling of the tanks and their valves.
The third tank uses a very small control valve, which is designed to make only the smallest corrections to the pH. If the pH of the liquid coming into the third tank is too high, then the controller will be neutralise the influent effectively, and the pH of the effluent will rise. This comes directly from the saturation limits of the control valve.
Even though this simulation concludes the example, this is not the final solution of the problem. There are many complex issues in industrial pH control, which will not be discussed here.