You are here : Control System Design - Index | Book Contents | Chapter 10

10. Internal Model Principle, Feedforward and Cascade Structures

Preview

The analysis in previous chapters has focused on feedback loop properties and feedback controller synthesis. In this chapter we will extend the scope of the analysis to focus on two further important aspects, namely: exact compensation of certain types of deterministic disturbances and exact tracking of particular reference signals. We will show that, compared to relying solely on feedback, the use of feedforward and or cascade structures offers advantages in many cases. We also generalize the idea of integral action to more general classes of disturbance compensators.

Summary
  • This chapter focuses the discussion of the previous chapter on a number of special topics with high application value:
    • internal disturbance models: compensation for classes of references and disturbances.
    • feedforward
    • cascade control
    • two-degree of freedom architectures
       
  • Signal models
    • Certain classes of reference or disturbance signals can be modeled explicitly by their Laplace transform:
      Signal Type Transform
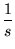      Step $\dfrac {a_1s+1}{s^2}$
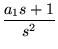      Ramp $\dfrac {a_2s^2+a_1s+1}{s^3}$
      Parabola
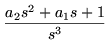      Sinusoid
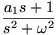    • Such references (disturbances) can be asymptotically tracked (rejected) if and only if the closed loop contains the respective transform in the sensitivity S0.
       
    • This is equivalent to having imagined the transforms being (unstable) poles of the open-loop and stabilizing them with the controller.
       
    • In summary, the internal model principle augments poles to the open loop gain function Go(s)C(s). However, this implies that the same design trade-offs apply as if these poles had been in the plant to begin with.
       
    • Thus internal model control is not cost free but must be considered as part of the design trade-off considerations.
       
  • Reference feedforward
    • A simple but very effective technique for improving responses to setpoint changes is prefiltering the setpoint (Figure 10.9).
       
    • This is the so called the two-degree-of-freedom (two d.o.f.) architecture since the prefilter H provides an additional design freedom. If, for example, there is significant measurement noise, then the loop must not be designed with too high a bandwidth. In this situation, reference tracking can be sped up with the prefilter.
       
    • Also, if the reference contains high-frequency components (such as step changes, for example), which are anyhow beyond the bandwidth of the loop, then one might as well filter them so not to excite uncertainties and actuators with them unnecessarily.
       
    • It is important to note, however, that design inadequacies in the loop (such as poor stability or performance) cannot be compensated by the prefilter. This is due to the fact that the prefilter does not affect the loop dynamics excited by disturbances.
       
      Figure 10.9: Two degree of freedom architecture for improved tracking
      \begin{figure} \end{figure}
       
    • Disturbance feedforward The trade-offs regarding sensitivities to reference, measurement noise, input-and output disturbances as discussed in the previous chapters refer to the case when these disturbances are technically or economically not measurable. Measurable disturbances can be compensated for explicitly (Figure 10.10), thus relaxing one of the trade-off constraints and giving the design more flexibility.
       
      Figure 10.10: Disturbance feedforward structure
      \begin{figure} \end{figure}
       
  • Cascade Control
    • Cascade control is a well-proven technique applicable when two or more systems feed sequentially into each other (Figure 10.11).
       
    • All previously discussed design trade-offs and insights apply.
       
    • If the inner loop (C2 in Fig. 10.11) were not utilized, then the outer controller (C1 in Fig. 10.12) would- implicitly or explicitly- estimate y1 as an internal state of the overall system ( Go1Go2). This estimate, however, would inherit the model-uncertainty associated with Go2. Therefore, utilizing the available measurement of y1 reduces the overall uncertainty and one can achieve the associated benefits.
     
    Figure 10.12: Cascade control structure
    \begin{figure} \end{figure}