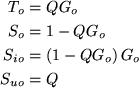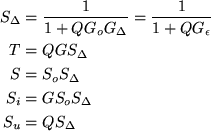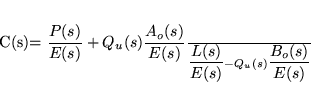You are here : Control System Design - Index | Book Contents | Chapter 15

15. SISO Controller Parameterisations

Preview

Up to this point in the book we have seen many different methods for designing controllers of different types. On reading all of this, one might be tempted to ask if there wasn't some easy way that one could specify all possible controllers that, at least, stabilized a given system. This sounds, at first glance a formidable task. However, we will show in this chapter that it is actually quite easy to give a relatively straightforward description of all stabilizing controllers for both open loop stable and unstable linear plants. This leads to an affine parameterization of all possible nominal sensitivity functions. This affine structure, in turn, gives valuable insights into the control problem and opens the door to various optimization based strategies for design. The main ideas presented in this chapter include

  • motivation for the affine parameterization and the idea of open loop inversion
  • affine parameterization and Internal Model Control
  • affine parameterization and performance specifications
  • PID synthesis using the affine parameterization
  • control of time delayed plants and affine parameterization. Connections with the Smith controller.
  • interpolation to remove undesirable open loop poles

Summary
  • The previous part of the book established that closed loop properties are interlocked in a network of trade offs. Hence, tuning for one property automatically impacts on other properties. This necessitates an understanding of the interrelations and conscious trade-off decisions.
     
  • The fundamental laws of trade-off presented in previous chapters allow one to both identify unachievable specifications as well as to establish where further effort is warranted or wasted.
     
  • However, when pushing a design maximally towards a subtle trade-off, the earlier formulation of the fundamental laws falls short because it is difficult to push the performance of a design by tuning in terms of controller numerator and denominator: The impact on the trade-off determining sensitivity-poles and zeros is very nonlinear, complex and subtle.
     
  • This shortcoming raises the need for an alternative controller representation that
    • allows one to design more explicitly in terms of the quantities of interest (the sensitivities),
    • makes stability explicit, and
    • makes the impact of the controller on the trade-offs explicit.
       
  • This need is met by the affine parameterization, also known as Youla parameterization
     
  • Summary of results for stable systems:
    • C = Q(1 - QGo)-1, where the design is carried out by designing the transfer function Q
    • Nominal sensitivities:

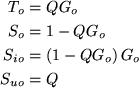
\begin{align}T_o&=QG_o\\ S_o&=1-QG_o\\ S_{io}&=\left( 1-QG_o\right) G_o \\ S_{uo}&=Q \end{align}

    • Achieved sensitivities (See the definitions of modeling errors in section 3.9):

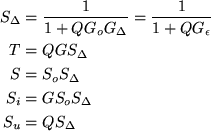
\begin{align}S_\Delta &=\frac 1{1+QG_oG_\Delta }=\frac 1{1+QG_\epsilon } \\ T... ... \\ S&=S_oS_\Delta \\ S_i&=GS_oS_\Delta \\ S_u&=QS_\Delta \end{align}

  • Observe the following advantages of the affine parameterization:
    • nominal stability is explicit
    • the known quantity Go and the quantity sought by the control engineer (Q) occur in the highly insightful relation To= QGo (multiplicative in the frequency domain); whether a designer chooses to work in this quantity from the beginning or prefers to start with a synthesis technique and then convert, the simple multiplicative relation QGo provides deep insights into the trade-offs of a particular problem and provides a very direct means of pushing the design by shaping Q
    • the sensitivities are affine in Q, which is a great advantage for synthesis techniques relying on numerical minimization of a criterion (see Chapter 16 for a detailed discussion of optimization methods which exploit this parameterization)
       
  • The following points are important to avoid some common misconceptions:
    • the associated trade-offs are not a consequence of the affine parameterization: they are perfectly general and hold for any linear time invariant controller including LQR, PID, pole placement based, $H_\infty $, etc.
    • we have used the affine parameterization to make the general trade-offs more visible and to provide a direct means for the control engineer to make trade-off decisions; this should not be confused with synthesis techniques that make particular choices in the affine parameterization to synthesize a controller
    • the fact that Q must approximate the inverse of the model at frequencies where the sensitivity is meant to be small is perfectly general and highlights the fundamental importance of inversion in control. This does not necessarily mean that the controller, C, must contain this approximate inverse as a factor and should not be confused with the pros and cons of that particular design choice
       
  • PI and PID design based on affine parameterization.
    • PI and PID controllers are traditionally tuned in terms of their parameters.
    • However, systematic design, trade-off decisions and deciding whether a PI(D) is sufficient or not, is significantly easier in the model-based affine structure.
    • Inserting a first order model into the affine structure automatically generates a PI controller.
    • Inserting a second order model into the Q-structure automatically generates a PID controller.
    • All trade-offs and insights of the previous chapters also apply to PID based control loops.
    • Whether a PI(D) is sufficient for a particular process is directly related to whether or not a first (second) order model can approximate the process well up to the frequencies where performance is limited by other factors such as delays, actuator saturations, sensor noise or fundamentally unknown dynamics.
    • The first and second order models are easily obtained from step response models (Chapter 3).
    • The chapter provides explicit formulas for first-order, time-delay, second order and integrating processes.
    • Using this method, the control engineer works directly in terms of observable process properties (rise time, gain, etc) and closed loop parameters providing an insightful basis for making trade-off decisions. The PI(D) parameters follow automatically.
    • Since the PI(D) parameter formulas are provided explicitly in terms of physical process parameters, the PI(D) gains can be scheduled to measurably changing parameters without extra effort (it is possible, for example, to schedule for a speed-dependent time-delay).
    • The approach does not preempt the design choice of canceling or shifting the open-loop poles - both are possible and associated with different trade-offs.
       
  • Summary of results for systems having time-delays:
    • The key issue is that delays cannot be inverted.
    • In that sense, delays are related to NMP plant zeros, which cannot be stably inverted either.
    • A delay of magnitude T, causes similar trade-offs as an unstable zero at s=T/2.
    • An early controller conceived to deal with the non-invertibility of delays is the famous Smith-predictor.
    • The trade-offs made in the Smith-predictor can be nicely analyzed in the affine structure. Indeed, the structures are very similar. Caution should be exercised, however, not to confuse the generic controller representation of the affine parameterization with the particular synthesis technique of the Smith-predictor.
       
  • Summary of results for unstable systems:
    • All stabilizing controllers for an unstable plant have the form
       
      \begin{displaymath} C(s)=\frac{\dfrac{P(s)}{E(s)}+Q_u(s)\dfrac{A_o(s)}{E(s)}} {\dfrac{L(s)}{E(s)}-Q_u(s)\dfrac{B_o(s)}{E(s)}} \end{displaymath}
       
      & where Qu(s) is any proper rational stable transfer function.
       
    • Polynomials Ao(s), Bo(s), E(s), P(s) and L(s) satisfy
       
      Ao(s)L(s) + Bo(s)P(s) = E(s)F(s)
       
      where E(s) and F(s) are polynomials of suitable degrees which are arbitrary, save that they must have desirable zeros.
    • Any stabilizing controller can be used to obtain an initial set of polynomials {E(s), P(s), L(s)}