You are here : Control System Design - Index | Book Contents | Chapter 20

20. Analysis of MIMO Control loops

Preview

In previous chapters we have focused on single-input, single-output problems. Other signals in the control loop have been considered as disturbances. However it frequently happens that what we have designated as disturbances in a given control loop, are signals originating in other loops, and vice-versa. This phenomenon is known as interaction or coupling.   In some cases, interaction can be ignored, either because the coupling signals are weak or because a clear time scale or, frequency scale separation exists. However, in other cases it may be necessary to consider all signals simultaneously. This leads us to consider multi-input multi-output (or MIMO) architectures.

A useful way to describe and refer to the problem of interaction is to borrow models and terminology from communication theory. If we assume that a MIMO system is square (same number of inputs and outputs), all inputs and outputs in the system can be paired. Then, the question of controlling every output yi(t), via manipulation of an input ui(t), in the presence of interactions, is similar to a communication channel, where interactions can be represented as channel crosstalk.   The idea can be extended to any square MIMO system, including complete control loops, where the transmitter is, say reference ri(k), and the receiver is output yi(k).

Throughout this chapter we will adhere to the convention used in the rest of the book, to use boldface type to denote matrices.

Summary
  • In previous chapters we have considered the problem of controlling a single output by manipulating a single input (SISO).
     
  • Many control problems, however, require that multiple outputs be controlled simultaneously; and to do so, multiple inputs must be manipulated -usually subtly orchestrated (MIMO):
    • Aircraft autopilot example: speed, altitude, pitch, roll and yaw angles must be maintained and; throttle, several rudders and flaps are available as control variables.
    • Chemical process example: yield, and throughput must be regulated and; thermal energy, valve actuators and various utilities are available as control variables.
       
  • The key difficulty in achieving the necessary orchestration of input is due to multivariable interactions, also known as coupling.
     
  • From an input-output point of view, two fundamental phenomena arise from coupling (see Figure 20.7):
    • a single input affects several outputs: dispersion.
    • several inputs affect a single output: directionality.

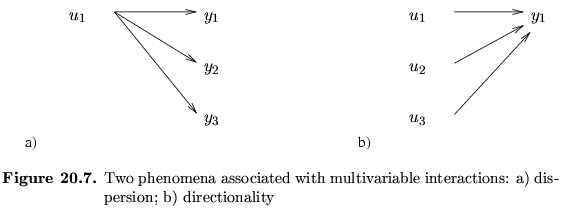
\begin{figure} \leavevmode \hangcaption{Two phenomena associated with multivariable interactions: a) dispersion; b) directionality} \end{figure}

  • Multivariable interactions in the form of dispersion and directionality add substantial complexity to MIMO control.
     
  • There are several ways to quantify interactions in multivariable systems, including their structure and their strength.
    • Interactions can have a completely general structure (every input potentially affects every output) or display a particular patterns such as triangular or dominant diagonal; they can also display frequency-dependent patterns such as being statically decoupled or band-decoupled.
    • The lower the strength of interaction, the more a system behaves like a set of independent systems which can be analyzed and controlled separately.
    • Weak coupling can occur due to the nature of the interacting dynamics, or due to a separation in frequency range or time scale.
    • The stronger the interaction, the more it becomes important to view the multiple-input multiple-output system and its interactions as a whole.
    • Compared to the SISO techniques discussed so far, viewing the MIMO systems and its interactions as whole requires generalized synthesis and design techniques and insight. These are the topics of the following two chapters.
       
  • Both state space and transfer function models can be generalized to MIMO models.
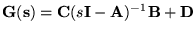  • The MIMO transfer function matrix can be obtained from a state space model by $\ensuremath{\mathbf{G(s)}} =\ensuremath{\mathbf{C}} (s\ensuremath{\mathbf{I}} -\ensuremath{\mathbf{A}} )^{-1}\ensuremath{\mathbf{B}} +\ensuremath{\mathbf{D}} $.
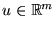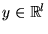  • In general, if the model has m inputs, $u \in \mathbb{R} ^m$, and l outputs, $y \in \mathbb{R} ^l$, then:
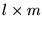    • the transfer function matrix consists of an $l\times m$ matrix of SISO transfer functions.
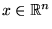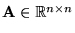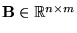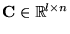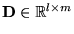    • for an n-dimensional state vector, $x \in \mathbb{R} ^n$, the state space model matrices have dimensions $\ensuremath{\mathbf{A}}\in \mathbb{R} ^{n\times n}$, $\ensuremath{\mathbf{B}}\in \mathbb{R} ^{n\times m}$, $\ensuremath{\mathbf{C}}\in \mathbb{R} ^{l\times n}$, $\ensuremath{\mathbf{D}}\in \mathbb{R} ^{l\times m}$.
       
  • Some MIMO model properties and analysis results generalize quite straightforwardly from SISO theory:
    • similarity transformations among state space realizations
    • observability and controllability
    • poles
       
  • Other MIMO properties, usually due to dispersion, directionality and the fact that matrices do not commute, are more subtle or complex than their SISO counterpart, e.g.
    • zeros
    • left and right matrix fractions.