You are here : Control System Design - Index | Book Contents | Chapter 24

24. Fundamental Design Limitations in MIMO Control

Preview

The best way to learn about real design issues is to become involved in practical applications. Hopefully, the reader may have gained some feeling for the lateral thinking that is typically needed in all real world problems from reading the various case studies that we have presented. In particular, we point to the 5 MIMO case studies described in Chapter 22.

In this chapter, we will adopt a more abstract stance and extend the design insights of Chapters 8 and 9 to the MIMO case. As a prelude to this, we recall that in Chapter 17 we saw that by a combination of an observer and state estimate feedback, the closed loop poles of a MIMO system can be exactly (or approximately) assigned depending on the synthesis method used. However, as in the SISO case, this leaves open two key questions; namely, where should the poles be placed and what are the associated sensitivity trade-off issues. This raises fundamental design issues which are the MIMO versions of the topics discussed in Chapters 8 and 9.

It has been shown in Chapters 8 and 9 that the open loop properties of a SISO plant impose fundamental and unavoidable constraints on the closed loop characteristics that are achievable. For example, we have seen that, for a one degree of freedom loop, a double integrator in the open loop transfer function implies that the integral of the error due to a step reference change must be zero. We have also seen that real RHP zeros necessarily imply undershoot in the response to a step reference change.

As might be expected, similar concepts apply to multivariable systems. However, whereas in SISO systems, one has only the frequency (or time) axis along which to deal with the constraints, in MIMO systems there is also a spatial dimension, i.e. one can trade off limitations between different outputs as well as on a frequency by frequency basis. This means that it is necessary to also account for the interactions between outputs rather than simply being able to focus on one output at a time. These issues will be explored below.

Summary
  • Analogous to the SISO case, MIMO performance specifications can generally not be addressed independently from another, since they are linked by a web of trade-offs.
     
  • A number of the SISO fundamental algebraic laws of trade-off generalize rather directly to the MIMO case  
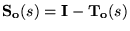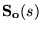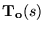    • $\ensuremath{\mathbf{S_o}(s)} =\ensuremath{\mathbf{I}} -\ensuremath{\mathbf{T_o}(s)} $ implying a trade-off between speed of response to a change in reference or rejecting disturbances ( \ensuremath{\mathbf{S_o}(s)} small) versus necessary control effort, sensitivity to measurement noise or modeling errors ( \ensuremath{\mathbf{T_o}(s)} small)
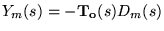    • $Y_{m}(s)=-\ensuremath{\mathbf{T_o}(s)} D_m(s)$ implying a trade-off between the bandwidth of the complementary sensitivity and sensitivity to measurement noise.
    • $\ensuremath{\mathbf{S_{uo}}(s)} =[\ensuremath{\mathbf{G_o}(s)} ]^{-1}\ensuremath{\mathbf{T_o}(s)} $ implying that a complementary sensitivity with bandwidth significantly higher than the open loop will generate large control signals.
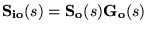    • $\ensuremath{\mathbf{S_{io}}(s)} =\ensuremath{\mathbf{S_o}(s)}\ensuremath{\mathbf{G_o}(s)} $ implying a trade-off between input and output disturbances.
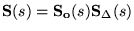    • $\ensuremath{\mathbf{S}(s)} = \ensuremath{\mathbf{S_{o}}(s)}\ensuremath{\mathbf{S_{\Delta}}(s)} $ where $\ensuremath{\mathbf{S_{\Delta}}(s)} =[\ensuremath{\mathbf{I}} +\ensuremath{\mathbf{G_{\Delta l}}(s)}\ensuremath{\mathbf{T_o}(s)} ]^{-1}$ implying a trade-off between the complementary sensitivity and robustness to modeling errors.
       
  • There also exist frequency- and time-domain trade-offs due to unstable poles and zeros:
    • qualitatively they parallel the SISO results in that (in a MIMO measure) low bandwidth in conjunction with unstable poles is associated with increasing overshoot, whereas high bandwidth in conjunction with unstable zeros is associated with increasing undershoot
    • quantitatively, the measure in which the above is true is more complex than in the SISO case: the effects of under- and overshoot, as well as integral constraints, pertain to linear combinations of the MIMO channels.
       
  • MIMO systems are subject to the additional design specification of desired decoupling.
     
  • Decoupling is related to the time- and frequency-domain constraints via directionality:
    • The constraints due to open-loop NMP zeros with non-canonical directions can be isolated in a subset of outputs, if triangular decoupling is acceptable.
    • Alternatively, if dynamic decoupling is enforced, the constraint is dispersed over several channels.
       
  • Advantages and disadvantages of completely decentralized control, dynamical and triangular decoupling designs were illustrated with an industrial case study:
Sugar mill case study

Design

Advantage

Disadvantage
Decentralized Simpler SISO theory can be used Interactions are ignored; poor performance
Dynamic Decoupling Outputs can be controlled separately Both output must obey the lower bandwidth constraint due to one NMP zero
Triangular Decoupling Most important output decoupled and without NMP constraint The second (albeit less important) output is affected by the first output and NMP constraint.