You are here : Control System Design - Index | Book Contents | Chapter 25

25. MIMO Controller Parameterisations

Preview

In this chapter we will extend the SISO design methods of Chapter 15 to the MIMO case. We will find that many issues are common between the SISO and MIMO cases. However, there are distinctive issues in the MIMO case which warrant separate treatment. The key factor leading to these differences is once again the fact that MIMO systems have spatial coupling, i.e. each input can affect more than one output and each output can be affected by more than one input. The consequences of this are far reaching. Examples of the difficulties which arise from these interactions include stability, non minimum phase zeros with their directionality properties and tracking performance.

Notwithstanding these differences, the central issue in MIMO control system design still turns out to be that of (approximate) inversion. Again, because of interactions, inversion is more intricate than in the SISO case, and we will thus need to develop more sophisticated tools for achieving this objective.

Summary
  • The generalization of the affine parameterization for a stable multivariable model, 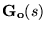\ensuremath{\mathbf{G_o}(s)}, is given by the controller representation $\ensuremath{\mathbf{C}(s)} =[\ensuremath{\mathbf{I}} -\ensuremath{\mathbf{Q}(s)... ...math{\mathbf{I}} -\ensuremath{\mathbf{G_o}(s)}\ensuremath{\mathbf{Q}(s)} ]^{-1}$
    yielding the nominal sensitivities
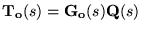
    $\ensuremath{\mathbf{T_o}(s)} =\ensuremath{\mathbf{G_o}(s)}\ensuremath{\mathbf{Q}(s)} $
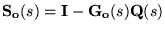
    $\ensuremath{\mathbf{S_o}(s)} =\ensuremath{\mathbf{I}} -\ensuremath{\mathbf{G_o}(s)}\ensuremath{\mathbf{Q}(s)} $
    $\ensuremath{\mathbf{S_{io}}(s)} =[\ensuremath{\mathbf{I}} -\ensuremath{\mathbf{G_o}(s)}\ensuremath{\mathbf{Q}(s)} ]\ensuremath{\mathbf{G_o}(s)} $
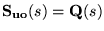
    $\ensuremath{\mathbf{S_{uo}}(s)} =\ensuremath{\mathbf{Q}(s)} $
     
  • The associated achieved sensitivity, when the controller is applied to 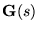\ensuremath{\mathbf{G}(s)} is given by
    $\ensuremath{\mathbf{S}(s)} =\ensuremath{\mathbf{S_o}(s)} [\ensuremath{\mathbf{I}} +\ensuremath{\mathbf{G_\epsilon}(s)}\ensuremath{\mathbf{Q}(s)} ]^{-1}$
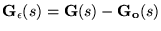    where $\ensuremath{\mathbf{G_\epsilon}(s)} = \ensuremath{\mathbf{G}(s)} -\ensuremath{\mathbf{G_o}(s)} $ is the additive modeling error.
     
  • In analogy to the SISO case, key advantages of the affine parameterization include
    • explicit stability of the nominal closed loop if and only if 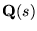\ensuremath{\mathbf{Q}(s)} is stable.
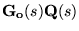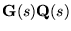    • highlighting the fundamental importance of invertibility, i.e. the achievable and achieved properties of $\ensuremath{\mathbf{G_o}(s)}\ensuremath{\mathbf{Q}(s)} $ and $\ensuremath{\mathbf{G}(s)}\ensuremath{\mathbf{Q}(s)} $.
    • Sensitivities that are affine in 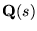\ensuremath{\mathbf{Q}(s)}; this facilitates criterion-based synthesis, which is particularly attractive for MIMO systems.
       
  • Again in analogy to the SISO case, inversion of stable MIMO systems involves the two key issues
    • relative degree; i.e., the structure of zeros at infinity
    • inverse stability; i.e., the structure of NMP zeros
       
  • Due to directionality, both of these attributes exhibit additional complexity in the MIMO case
     
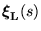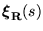  • The structure of zeros at infinity is captured by the left (right) interactor, $\ensuremath{\mathbf{\boldsymbol{\xi}_{L}}(s)} $ ( $\ensuremath{\mathbf{\boldsymbol{\xi}_{R}}(s)} $).
     
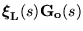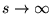  • Thus $\ensuremath{\mathbf{\boldsymbol{\xi}_{L}}(s)}\ensuremath{\mathbf{G_o}(s)} $ is biproper, i.e., its determinant is a non zero bounded quantity for $s\rightarrow \infty$.
     
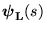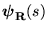  • The structure of NMP zeros is captured by the left (right) z-interactor, $\ensuremath{\mathbf{\boldsymbol{\psi}_{L}}(s)} $ ( $\ensuremath{\mathbf{\boldsymbol{\psi}_{R}}(s)} $).
     
  • Thus, analytically, 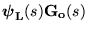$\ensuremath{\mathbf{\boldsymbol{\psi}_{L}}(s)}\ensuremath{\mathbf{G_o}(s)} $ is a realization of the inversely stable portion of the model (i.e., the equivalent to the minimum phase factors in the SISO case).
     
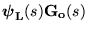
  • However, the realization $\ensuremath{\mathbf{\boldsymbol{\psi}_{L}}(s)}\ensuremath{\mathbf{G_o}(s)} $
    • is non minimal
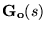    • generally involves cancellations of unstable pole-zero dynamics (the NMP zero dynamics of \ensuremath{\mathbf{G_o}(s)}).
       
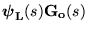
  • Thus, the realization $\ensuremath{\mathbf{\boldsymbol{\psi}_{L}}(s)}\ensuremath{\mathbf{G_o}(s)} $
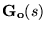
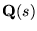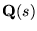
    • is useful for analyzing the fundamentally achievable properties of the key quantity \ensuremath{\mathbf{G_o}(s)} \ensuremath{\mathbf{Q}(s)}, subject to the stability of \ensuremath{\mathbf{Q}(s)}
    • is generally not suitable for either implementation or inverse implementation, as it involves unstable pole-zero cancellation.
       
  • A stable inverse suitable for implementation is generated by model matching which leads to a particular linear quadratic regulator (LQR) problem which is solvable via Riccati equations.
     
  • If the plant model is unstable, controller design can be carried out in two steps
    • pre-stabilization, for example via LQR
    • detailed design by applying the theory for stable models to the pre-stabilized system.
       
  • All of the above results can be interpreted equivalently in either a transfer function or a state space framework; for MIMO systems, the state space framework is particularly attractive for numerical implementation.