|
You are here : Control System Design - Index | Book Contents | Appendix C | Section C.4 C. Results from Analytic Function Theory
In the sequel, we will let |
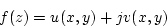 |
(C.4.1) |
Note that we also have
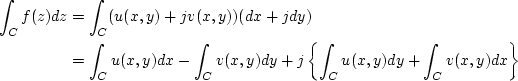
We then see that the previous results are immediately applicable to the real and imaginary parts of integrals of this type.
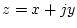 denote a complex variable. Note that
denote a complex variable. Note that  is not the argument in
the Z-transform, as used at other points in the book. Also, a
function
is not the argument in
the Z-transform, as used at other points in the book. Also, a
function 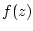 of a complex variable is equivalent to a function
of a complex variable is equivalent to a function
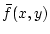 .
This will have real and imaginary parts
.
This will have real and imaginary parts 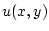 and
and 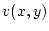 respectively.
respectively.