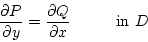|
You are here : Control System Design - Index | Book Contents | Appendix C | Section C.3 C. Results from Analytic Function Theory
|
 |
(C.3.1) |
where 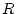 is the region bounded by
is the region bounded by  .
.
Proof
We first consider a simple case in which 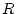 is representable in both
of the forms:
is representable in both
of the forms:
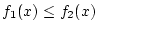 |
 |
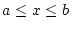 |
(C.3.2) |
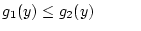 |
 |
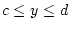 |
(C.3.3) |
Then
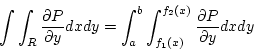 |
(C.3.4) |
One can now integrate to achieve
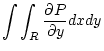 |
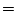 |
![$\displaystyle \int_a^b[P(x,f_2(x))-P(x,f_1(x))]dx$](appendixC-img53.png) |
(C.3.5) |
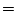 |
 |
(C.3.6) | |
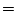 |
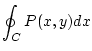 |
(C.3.7) |
By a similar argument,
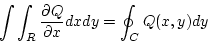 |
(C.3.8) |
For more complex regions, we decompose into simple regions as above. The result then follows.

We then have the following converse to Theorem C.3.
Theorem C.5
Let 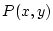 and
and  have continuous derivatives in
have continuous derivatives in  and let
and let
 be simply connected. If
be simply connected. If
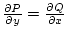 , then
, then
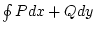 is
independent of path in
is
independent of path in  .
.
Proof
Suppose that
Then, by Green's Theorem (Theorem C.4),
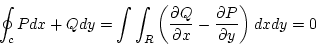 |
(C.3.10) |