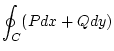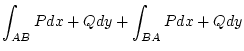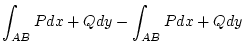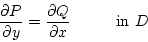|
You are here :
Control System Design - Index | Book Contents |
Appendix C
| Section C.2
C. Results from Analytic Function Theory
C.2 Independence of Path
Consider functions of two independent variables, 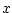 and
and 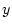 .
(The
reader can think of .
(The
reader can think of 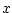 as the real axis and
as the real axis and 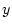 as the imaginary
axis.)
as the imaginary
axis.)
Let 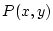 and
and  be two functions of
be two functions of 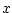 and
and 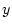 ,
continuous
in some domain ,
continuous
in some domain  .
Say we have a curve .
Say we have a curve  in
in  ,
described by the
parametric equations ,
described by the
parametric equations
 |
(C.2.1) |
We can then define the following line integrals along the path  from point from point 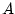 to point
to point 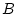 inside
inside  . .
Definition C.1
The line integral
 is said to be independent of the
path in is said to be independent of the
path in  if, for every pair of points if, for every pair of points 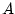 and and 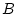 in in  , the
value of the integral is independent of the path followed from , the
value of the integral is independent of the path followed from 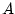 to to 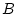 . .

We then have the following result.
Theorem C.1
If
 is independent of the path in is independent of the path in  , then there
exists a function , then there
exists a function 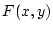 in in  such that such that
 |
(C.2.4) |
hold throughout  . Conversely, if a function . Conversely, if a function 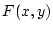 can
be found such that (C.2.4) hold, then can
be found such that (C.2.4) hold, then
 is independent of the path. is independent of the path.
Proof
Suppose that the integral is independent of the path in  .
Then,
choose a point .
Then,
choose a point 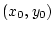 in
in  and let
and let 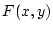 be defined as
follows
be defined as
follows
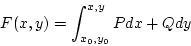 |
(C.2.5) |
where the integral is taken on an arbitrary path in  joining joining 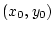 and
and 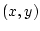 .
Because the integral is
independent of the path, the integral does indeed depend only on .
Because the integral is
independent of the path, the integral does indeed depend only on 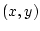 and defines the function
and defines the function 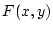 .
It remains to establish
(C.2.4). .
It remains to establish
(C.2.4).
Figure C.1:
Integration path
 |
For a particular 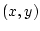 in
in  ,
choose ,
choose 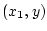 so that
so that 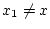 and so that the line segment from
and so that the line segment from 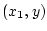 to
to 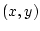 in
in  is as shown in Figure C.1. Because of independence
of the path, is as shown in Figure C.1. Because of independence
of the path,
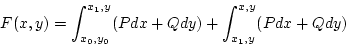 |
(C.2.6) |
We think of 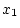 and
and 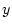 as being fixed while
as being fixed while 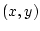 may vary
along the horizontal line segment. Thus
may vary
along the horizontal line segment. Thus 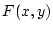 is being
considered as function of
is being
considered as function of 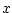 .
The first integral on the
right-hand side of (C.2.6) is then independent of .
The first integral on the
right-hand side of (C.2.6) is then independent of 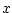 . .
Hence, for fixed 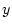 ,
we can write ,
we can write
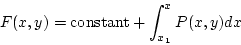 |
(C.2.7) |
The fundamental theorem of Calculus now gives
 |
(C.2.8) |
A similar argument shows that
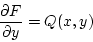 |
(C.2.9) |
Conversely, let (C.2.4) hold for some 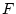 .
Then, with .
Then, with
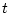 as a parameter,
as a parameter,
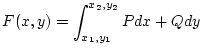 |
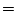 |
 |
(C.2.10) |
| |
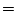 |
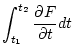 |
(C.2.11) |
| |
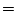 |
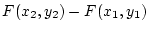 |
(C.2.12) |

Theorem C.2
If the integral
 is independent of the path in is independent of the path in  ,
then ,
then
 |
(C.2.13) |
on every closed path in  . Conversely if (C.2.13) holds
for every simple closed path in . Conversely if (C.2.13) holds
for every simple closed path in  , then , then
 is
independent of the path in is
independent of the path in  . .
Figure C.2:
Integration path
 |
Proof
Suppose that the integral is independent of the path. Let  be a
simple closed path in
be a
simple closed path in  ,
and divide ,
and divide  into arcs
into arcs 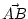 and
and
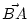 as in Figure C.2.
as in Figure C.2.
The converse result is established by reversing the above argument.

Theorem C.3
If 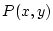 and and  have continuous partial derivatives in have continuous partial derivatives in  and and
 is independent of the path in is independent of the path in  , then , then
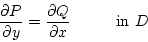 |
(C.2.16) |
Proof
By Theorem C.1, there exists a function 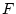 such
that (C.2.4) holds. Equation (C.2.16) follows
by partial differentiation.
such
that (C.2.4) holds. Equation (C.2.16) follows
by partial differentiation.

Actually, we will be particularly interested in the converse to Theorem C.3. However, this holds under slightly more
restrictive assumptions, namely a simply connected domain.
|
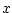 and
and 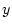 .
(The
reader can think of
.
(The
reader can think of 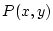 and
and  be two functions of
be two functions of  .
Say we have a curve
.
Say we have a curve  in
in 
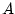 to point
to point 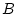 inside
inside 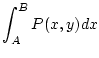
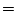
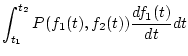
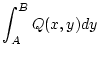
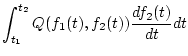
 is said to be independent of the
path
is said to be independent of the
path
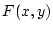 in
in 
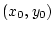 in
in 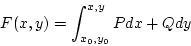
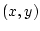 .
Because the integral is
independent of the path, the integral does indeed depend only on
.
Because the integral is
independent of the path, the integral does indeed depend only on 
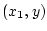 so that
so that 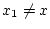 and so that the line segment from
and so that the line segment from 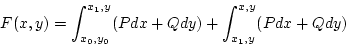
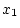 and
and 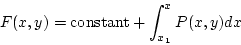

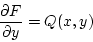
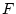 .
Then, with
.
Then, with
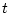 as a parameter,
as a parameter,
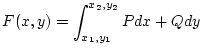

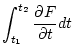
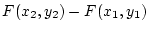


 and
and
 as in
as in