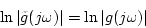|
You are here :
Control System Design - Index | Book Contents |
Appendix C
| Section C.8
C. Results from Analytic Function Theory
C.8.2 Poisson-Jensen Formula for the Half-Plane
Lemma C.1
Consider a function 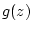 having the following properties having the following properties
- (i)
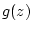 is analytic on the closed RHP;
is analytic on the closed RHP;
- (ii)
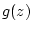 does not vanish on the imaginary axis;
does not vanish on the imaginary axis;
- (iii)
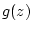 has zeros in the open RHP, located at
has zeros in the open RHP, located at
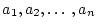 ; ;
- (iv)
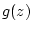 satisfies
satisfies
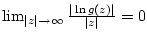 . .
Consider also a point
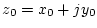 such that such that 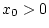 ; then ; then
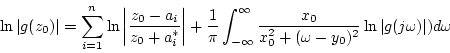 |
(C.8.13) |
Proof
Let
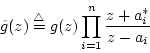 |
(C.8.14) |
Then,
 is analytic within the closed unit disk.
If we now apply Theorem C.9 to
is analytic within the closed unit disk.
If we now apply Theorem C.9 to
 ,
we obtain ,
we obtain
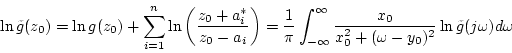 |
(C.8.15) |
We also recall that, if 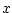 is any complex number, then
is any complex number, then
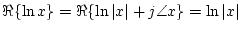 .
Thus, the result follows
upon equating real parts in the equation above and noting that .
Thus, the result follows
upon equating real parts in the equation above and noting that
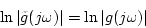 |
(C.8.16) |

|
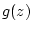 having the following properties
having the following properties
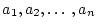 ;
;
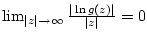 .
.
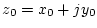 such that
such that 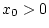 ; then
; then
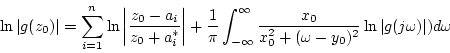
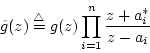
 is analytic within the closed unit disk.
If we now apply
is analytic within the closed unit disk.
If we now apply 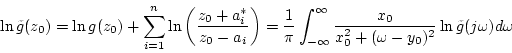
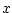 is any complex number, then
is any complex number, then
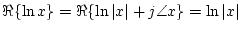 .
Thus, the result follows
upon equating real parts in the equation above and noting that
.
Thus, the result follows
upon equating real parts in the equation above and noting that