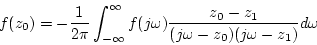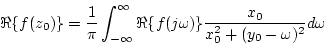|
You are here : Control System Design - Index | Book Contents | Appendix C | Section C.8 C. Results from Analytic Function Theory
|
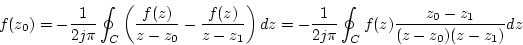 |
(C.8.7) |
Because
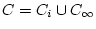 ,
the integral over
,
the integral over  can be
decomposed into the integral along the imaginary axis ,
can be
decomposed into the integral along the imaginary axis , 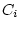 ,
and
the integral along the semicircle of infinite radius,
,
and
the integral along the semicircle of infinite radius, 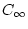 .
Because
.
Because 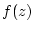 satisfies (C.8.3), this second integral
vanishes, because the factor
satisfies (C.8.3), this second integral
vanishes, because the factor
 is of order
is of order 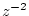 at
at 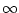 .
.
Then
The result follows upon replacing 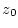 and
and  by their real;
and imaginary-part decompositions.
by their real;
and imaginary-part decompositions.

Remark C.1
One of the functions that satisfies
(C.8.3) but does not satisfy (C.8.1)
is
 , where
, where 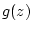 is a rational
function of relative degree
is a rational
function of relative degree 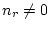 . We notice that, in this
case,
. We notice that, in this
case,
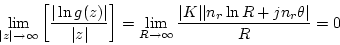 |
(C.8.9) |
where 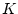 is a finite constant and
is a finite constant and 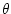 is an angle in
is an angle in
![$[-\frac{\pi}{2}, \frac{\pi}{2}] $](appendixC-img192.png) .
.
Remark C.2 Equation (C.8.4) equates two complex quantities. Thus, it also applies independently to their real and imaginary parts. In particular,
This observation is relevant to many interesting cases. For
instance, when 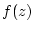 is as in remark C.1,
is as in remark C.1,
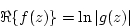 |
(C.8.11) |
For this particular case, and assuming that 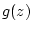 is a real function
of
is a real function
of  , and that
, and that  , we have that (C.8.10) becomes
, we have that (C.8.10) becomes
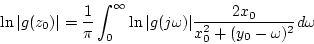 |
(C.8.12) |
where we have used the conjugate symmetry of 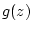 .
.
 .
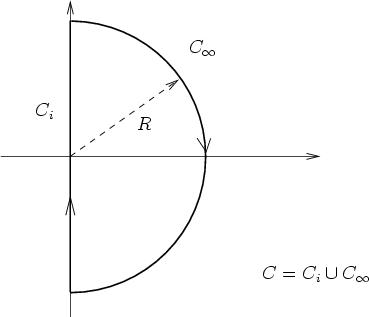
.  . This contour is shown in
. This contour is shown in 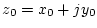 with
with 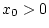 .
.
 ;
; 
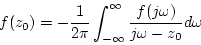
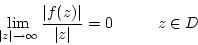
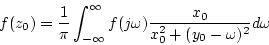
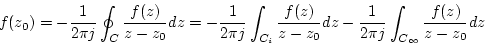
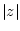 ,
i.e.,
,
i.e.,
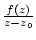 is like
is like 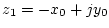 .
Then
.
Then
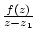 is analytic inside
is analytic inside