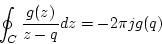|
You are here : Control System Design - Index | Book Contents | Appendix C | Section C.7 C. Results from Analytic Function TheoryC.7 Integrals Revisited
Theorem C.7 (Cauchy Integral Theorem)
If
where
ProofThis follows from the Cauchy-Riemann conditions together with Theorem C.2.
We are also interested in the value of integrals in various limiting situations. The following examples cover relevant cases.
We note that if
Example C.5
Assume that
Example C.6
Consider the function
This is proven as follows. On
We then use the fact that
Example C.7 Consider the function
and a semicircle,
This is proven as follows.
On
We also know that
Then
From this, by evaluation for
Example C.8 Consider the function
and a semicircle,
This is proven as follows.
On
We recall that, if
Moreover, for very large
Thus, in the limit, this quantity goes to zero for all positive
Example C.9 Consider the function
and a semicircle,
This result is obtained by noting that
and then applying the result in Example C.7.
Example C.10 Consider a function of the form
and
Thus, as
Example C.11
Consider, now,
We can now develop Cauchy's Integral Formula.
Say that
the
Consider the path shown in Figure C.3. Because
This leads to the following result.
Theorem C.8 (Cauchy's Integral Formula)
Let
We note that the residue of
|
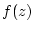 is analytic in some simply connected domain
is analytic in some simply connected domain  , then
, then
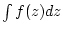 is independent of path in
is independent of path in 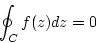
 is a simple closed path in
is a simple closed path in 
 is the length of a simple curve
is the length of a simple curve 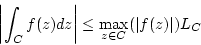
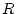 . The path length is then
. The path length is then 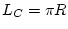 . Hence,
. Hence,
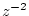 ,
then
,
then 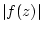 on
on 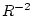 - hence, the integral on
- hence, the integral on  .
. ,
then
,
then 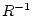 - then, the integral on
- then, the integral on 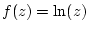 and an arc of a circle,
and an arc of a circle, 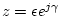 for
for
![$\gamma\in[-\gamma_1,\gamma_1]$](appendixC-img118.png) . Then
. Then

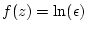 . Then
. Then
![\begin{displaymath}I_\epsilon=\lim_{\epsilon\rightarrow 0}
\left[(\gamma_2-\gamma_1)\epsilon\ln (\epsilon)\right ]
\end{displaymath}](appendixC-img121.png)
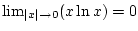 ,
and the result follows.
,
and the result follows.

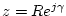 for
for
![$\gamma\in \left[- \frac{\pi}{2}, \frac{\pi}{2} \right]$](appendixC-img125.png) . Then, if
. Then, if

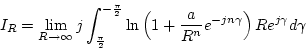

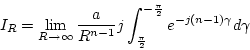
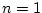 and for
and for 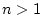 , the result
follows.
, the result
follows.

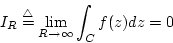
![\begin{displaymath}I_R= \lim_{R\rightarrow \infty}j\int_{\frac{\pi}{2}}^{-\frac{...
...\frac{z}{e^{z\tau}} \right )z
\right]
_{z=Re^{j\gamma}}d\gamma
\end{displaymath}](appendixC-img134.png)
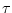 is a positive real number and
is a positive real number and
 , then
, then
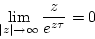
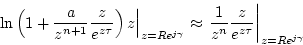
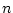 . The result then follows.
. The result then follows.
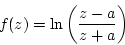
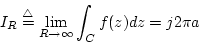

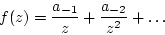
 for
for
![$\theta\in
[\theta_1, \theta_2]$](appendixC-img145.png) . Thus,
. Thus,
 , and
, and
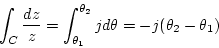
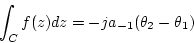
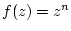 . If the path
. If the path 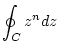
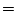
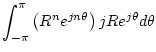
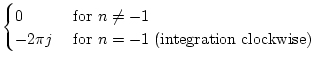
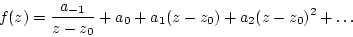
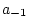 is called the residue of
is called the residue of 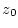 .
.
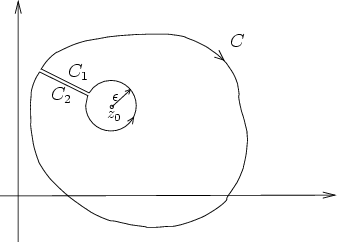
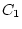 and
and 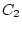 cancel. The anticlockwise circular integral around
cancel. The anticlockwise circular integral around 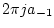 .
Hence, the integral around the outer curve
.
Hence, the integral around the outer curve 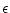 .
Thus,
.
Thus,

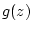 be analytic in a region. Let
be analytic in a region. Let 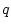 be a point inside the region.
Then
be a point inside the region.
Then
 has residue
has residue 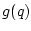 at
at 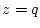 , and the
integral around any closed contour
, and the
integral around any closed contour