|
You are here : Control System Design - Index | Book Contents | Appendix C | Section C.6 C. Results from Analytic Function Theory
|
 |
(C.6.1) |
Furthermore
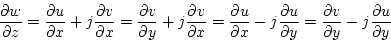 |
(C.6.2) |
Proof
Let 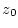 be a fixed point in
be a fixed point in  and let
and let
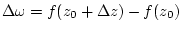 .
Because
.
Because 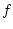 is analytic, we
have
is analytic, we
have
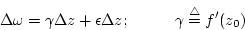 |
(C.6.3) |
where
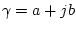 and
and 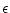 goes to zero as
goes to zero as  goes to
zero. Then
goes to
zero. Then
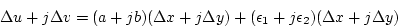 |
(C.6.4) |
So
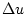 |
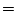 |
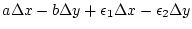 |
(C.6.5) |
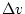 |
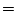 |
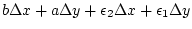 |
(C.6.6) |
Thus, in the limit, we can write
 |
(C.6.7) |
or
 |
(C.6.8) |

Actually, most functions that we will encounter will be analytic, provided the derivative exists. We illustrate this with some examples.
Example C.1
Consider the function  . Then
. Then
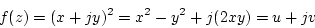 |
(C.6.9) |
The partial derivatives are
 |
(C.6.10) |
Hence, the function is clearly analytic.
Example C.2
Consider 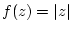 .
.
This function is not analytic, because 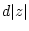 is a real quantity
and, hence,
is a real quantity
and, hence,
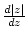 will depend on the direction of
will depend on the direction of
 .
.
Example C.3 Consider a rational function of the form:
![\begin{displaymath}\frac{\partial W}{\partial z}=\frac{1}{D^2(z)}
\left[ D(z)\fr...
...(z)}{\partial z}-N(z)
\frac{\partial D(z)}{\partial z} \right]
\end{displaymath}](appendixC-img99.png) |
(C.6.12) |
These derivatives clearly exist, save when 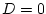 ,
that is at the
poles of
,
that is at the
poles of 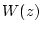 .
.
Example C.4
Consider the same function 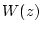 defined in
(C.6.11). Then
defined in
(C.6.11). Then
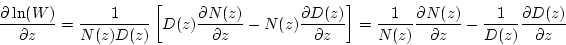 |
(C.6.13) |
Hence,
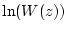 is analytic, save at the poles and zeros of
is analytic, save at the poles and zeros of
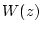 .
.
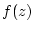 is said to be analytic in a domain
is said to be analytic in a domain  is analytic in
is analytic in 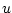 and
and 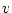 have continuous
partial derivatives satisfying the Cauchy-Riemman conditions.
have continuous
partial derivatives satisfying the Cauchy-Riemman conditions.
