| Notation |
Meaning |
|---|
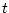 |
Continuous-time variable |
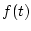 |
Continuous-time signal |
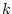 |
Discrete-time variable |
![$\{f[k]\}$](appendixa-img4.png) |
Discrete-time sequence |
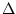 |
Sampling period |
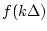 |
Sampled version of
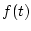 |
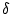 |
Delta operator |
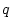 |
forward shift operator |
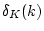 |
Kronecker delta |
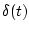 |
Dirac delta |
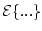 |
Expected value of ... |
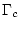 |
Controllability matrix in state space description |
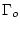 |
Observability matrix in state space description |
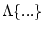 |
Set of eigenvalues of matrix ... |
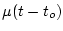 |
unit step (continuous time) at time 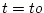 |
![$\mu
[k-k_o]$](appendixa-img17.png) |
unit step (discrete time) at time 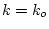 |
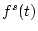 |
Dirac impulse-sampled version of 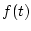 |
![$\ensuremath{{\cal{F}}\left[...\right]} $](appendixa-img20.png) |
Fourier
transform of ... |
![$\ensuremath{{\cal{L}}\left[...\right]} $](appendixa-img21.png) |
Laplace transform of ... |
![$\ensuremath{{\cal{D}}\left[...\right]} $](appendixa-img22.png) |
Delta-transform of ... |
![$\ensuremath{{\cal{Z}}\left[...\right]} $](appendixa-img23.png) |
Z-transform of
... |
![$\ensuremath{{\cal{F}}^{-1}\left[...\right]} $](appendixa-img24.png) |
inverse Fourier transform of ... |
![$\ensuremath{{\cal{L}}^{-1}\left[...\right]} $](appendixa-img25.png) |
inverse Laplace transform of ... |
![$\ensuremath{{\cal{D}}^{-1}\left[...\right]} $](appendixa-img26.png) |
inverse Delta-transform of ... |
![$\ensuremath{{\cal{Z}}^{-1}\left[...\right]} $](appendixa-img27.png) |
inverse
Z-transform of ... |
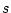 |
Laplace-transform complex variable |
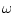 |
angular frequency |
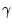 |
Delta-transform complex
variable |
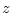 |
Z-transform complex variable |
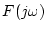 |
Fourier
transform of 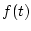 |
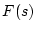 |
Laplace transform of 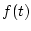 |
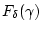 |
Delta-transform of ![$\{f[k]\}$](appendixa-img4.png) |
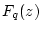 |
Z-transform of ![$\{f[k]\}$](appendixa-img4.png) |
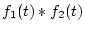 |
Time
convolution of 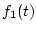 and
and 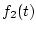 |
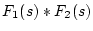 |
Complex
convolution of 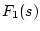 and
and 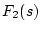 |
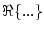 |
real part of
... |
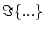 |
imaginary part of ... |
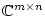 |
set of all 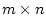 matrices with complex entries
matrices with complex entries |
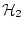 |
Hilbert space of those functions square-integrable
along the imaginary axis and analytic in the right-half plane |
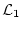 |
Hilbert space of those functions absolutely
integrable along the imaginary axis |
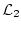 |
Hilbert space
of those functions square-integrable along the imaginary axis. |
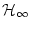 |
Hilbert space of those functions bounded along
the imaginary axis and analytic in the right-half plane |
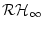 |
Hilbert space of those rational
functions bounded along the imaginary axis and analytic in the
right-half plane |
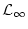 |
Hilbert space of those
functions bounded along the imaginary axis. |
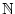 |
set of
all natural numbers |
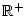 |
set of real numbers larger
than zero |
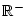 |
set of real numbers smaller than zero |
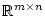 |
set of all 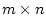 matrices with real
entries
matrices with real
entries |
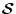 |
set of all real rational functions with
(finite) poles strictly inside the LHP |
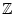 |
set of all
integer numbers |
![$[\alpha_{ik}]$](appendixa-img58.png) |
Matrix where the element in the
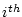 row and
row and 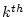 column is denoted by
column is denoted by
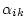 |
![$[\ensuremath{\mathbf{A}} ]_{ik}$](appendixa-img62.png) |
element in the 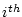 row and
row and 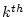 of
matrix
of
matrix
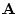 |
![$[\ensuremath{\mathbf{A}} ]_{i*}$](appendixa-img64.png) |
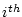 row of matrix
row of matrix
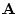 |
![$
[\ensuremath{\mathbf{A}} ]_{*k}$](appendixa-img65.png) |
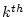 columm of matrix
columm of matrix
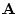 |
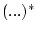 |
complex conjugate of ... |
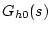 |
transfer function of a zero-order hold |
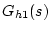 |
transfer function of a first-order hold |
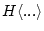 |
operator notation, i.e.  operates on ...
operates on ... |
 |
composite operators, i.e.,
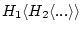 |
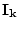 |
identity matrix in
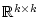 |
| d.c. |
direct current, i.e.,
zero-frequency signal |
| d.o.f. |
degrees of freedom |
| CTARE |
Continuous-Time Algebraic Riccati Equation |
| DTARE |
Discrete-Time
Algebraic Riccati Equation |
| CTDRE |
Continuous-Time Dynamic
Riccati Equation |
| DTDRE |
Discrete-Time Dynamic Riccati Equation |
| IMC |
Internal Model Control |
| IMP |
Internal Model Principle |
| LHP |
left half-plane |
| OLHP |
open left half-plane |
| RHP |
right half-
plane |
| ORHP |
open right-half plane |
| NMP |
nonminimum phase |
| MFD |
Matrix fraction description |
| LMFD |
Left matrix fraction
description |
| RMFD |
Right matrix fraction description |
| LTI |
Linear time invariant |
| LQR |
Linear quadratic regulator |
| w.r.t |
with respect to ... |
| |
|
|---|