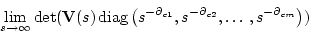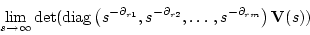|
You are here : Control System Design - Index | Book Contents | Appendix B | Section B.2 B. Smith McMillan FormsB.2 Polynomial MatricesMultivariable transfer functions depend on polynomial matrices. There are a number of related terms that are used. Some of these are introduced here:
Definition B.2 A polynomial matrix
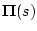 is said to be a unimodular
matrix if its determinant is a constant.
Clearly, the inverse of a unimodular matrix is also a unimodular matrix.
is said to be a unimodular
matrix if its determinant is a constant.
Clearly, the inverse of a unimodular matrix is also a unimodular matrix.
Definition B.3
An elementary operation
on a polynomial matrix is one of the
following three operations:
Definition B.4
A left (right) elementary matrix is a matrix such that, when
it multiplies from the left (right) a polynomial matrix, then it
performs a row (column) elementary operation on the polynomial
matrix. All elementary matrices are unimodular.
Definition B.5
Two polynomial matrices
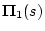 and
and
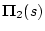 are equivalent matrices,
if there exist sets of left and right elementary matrices,
are equivalent matrices,
if there exist sets of left and right elementary matrices,
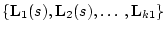 and
and
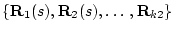 ,
respectively, such that ,
respectively, such that
Definition B.6 The rank of a
polynomial matrix
is the rank of the matrix almost
everywhere in
Definition B.7 Two polynomial matrices
Definition B.8 The degree
|
![$\ensuremath{\mathbf{\ensuremath{\boldsymbol{\Pi}}}(s)} =[p_{ik}(s)]\in {\mathbb{R} }^{n_1\times n_2}$](appendixb-img1.png) is a polynomial
matrix
is a polynomial
matrix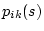 is a polynomial in
is a polynomial in
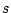 ,
for
,
for
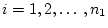 and
and
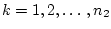 .
.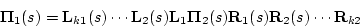
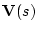 and
and
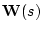 having the same
number of columns (rows) are right (left) coprime if all
common right (left) factors are unimodular
matrices.
having the same
number of columns (rows) are right (left) coprime if all
common right (left) factors are unimodular
matrices.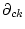 (
(
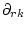 )
of the
)
of the 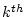 column (row)
column (row)
![$[\ensuremath{\mathbf{V}(s)} ]_{*k}$](appendixb-img18.png) (
(
![$[\ensuremath{\mathbf{V}(s)} ]_{k*}$](appendixb-img19.png) )
of a polynomial
matrix
)
of a polynomial
matrix
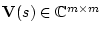 is column proper
is column proper