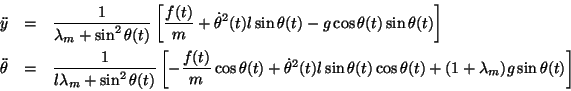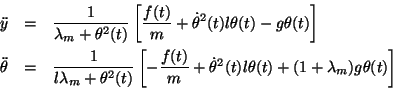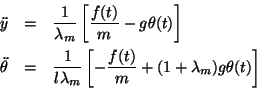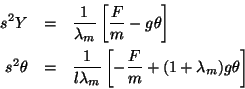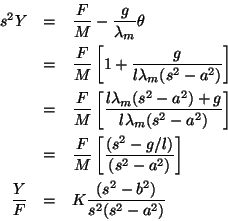You are here : Control System Design - Index | Simulations | Inverted Pendulum | Part 1

Inverted Pendulum Tutorial - Part 1

System Model

The modelling of the inverted pendulum system comes straight from simple Newtonian physics. (Note: Modelling is covered in chapter 3 and chapter 4.) This gives us the following equations:

equation

To make the model useful for us, we need to linearize it. Chapter 2 gives one possible procedure for this, but a more heuristic one will be presented here (which incidentally gives the same result). We first recognise that sin alpha = alpha and cos alpha = 1 when alpha is small. This approximation yields:

equation

This model is for small variations of theta only (i.e. a small signal model) so we assume that theta is small enough such that theta^2 = 0 and thetadot^2 = 0. Then,

equation

We next take the Laplace transform of these equations (as described in section 3.3).

equation

Now, working with the second equation,

equation

Note that lambda_m = M/m and let a^2= (1+lambda_m)g / lambda_m, so

equation

Recalling the definition of a, we see that

equation

Where b2 = g / l. Using M = m = 0.5, l = 1 and g = 10 we get the following transfer function:

We can see immediately that there is one non-minimum phase zero and an unstable pole. Because of this pole, the system is open-loop unstable (i.e. if we nudge the cart a bit, the mass will fall over). Next, we try to control the inverted pendulum system based on the linear model we have just made.