|
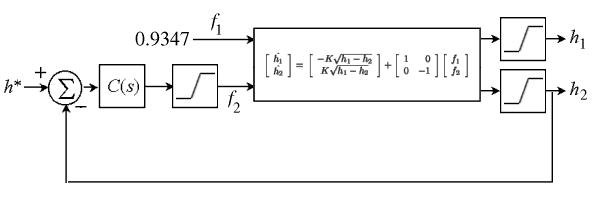
You are here : Control System Design - Index | Simulations | Tank Level | Part 2 Tank Level Tutorial - Part 2The JAVA applet below is a simulation of the above tank system. The controller used in the previous simulation (and this next one) was a simple SISO PI controller forming a loop around the height h2. The controller parameters are kp = -0.3 and ki = -0.007. Pump 1 is given a constant voltage so that the flow into tank 1 is always f1 = 0.9347. There are two important physical limitations on the system: the tank heights cannot be more than 100% or less than 0% and the flow out of tank 2 cannot be negative (no water can be pumped into the tank) or more than 10% per second. Because of this saturation of the actuator, an anti-windup controller has been implemented (see Chapter 14). (Another limitation of the model is that h1 must always be larger than h2, but this can be overcome by replacing
with
when h2 is larger, since in this case f12 will be negative.) The block diagram for the closed loop system is shown below:
As before, the graph has a vertical scale of 25% per division and a horizontal scale of 10 sec per division. It shows the set-point (the orange trace), the actual h1 (the blue trace), the estimated h1 (the red trace) and the actual h2 (the green trace). Pressing the "Change Parameters" button allows you to change the same parameters as in the previous example plus the controller parameters. Designing a controller for both the tank heights will not be covered by this discussion, but you might like to try this interesting problem yourself.
|
||||||||||