|
You are here : Control System Design - Index | Book Contents | Appendix C | Section C.8 C. Results from Analytic Function TheoryC.8.4 Poisson-Jensen Formula for the Unit Disk
Lemma C.2
Consider a function
Consider also a point
ProofLet
Then
We also recall that, if
Theorem C.11 (Jensen's formula for the unit disk)
Let
If
then
ProofWe first note that
We thus have that
The result follows upon subtracting Equation (C.8.35) from (C.8.34), and noting that
Remark C.3
Further insights can be obtained from Equation (C.8.32) if we assume that, in (C.8.31),
then
Thus,
This allows Equation (C.8.32) to be rewritten as
where
|
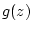 having the following properties:
having the following properties:
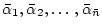 .
.
 such that
such that 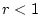 ; then
; then
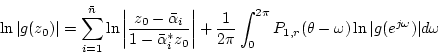
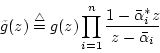
 is analytic on the closed unit disk. If we
now apply
is analytic on the closed unit disk. If we
now apply 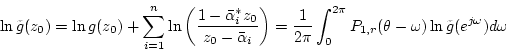
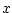 is any complex number, then
is any complex number, then
 .
Thus the result follows upon equating real
parts in the equation above and noting that
.
Thus the result follows upon equating real
parts in the equation above and noting that
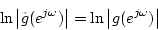

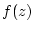 and
and 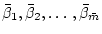 respectively, where none
of these zeros lie on the unit circle.
respectively, where none
of these zeros lie on the unit circle.
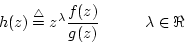
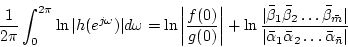
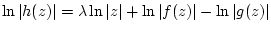 .
We then apply the Poisson-Jensen formula to
.
We then apply the Poisson-Jensen formula to 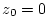 to obtain
to obtain

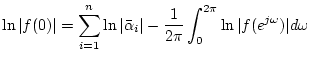
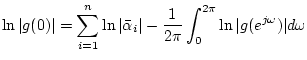
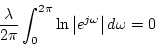
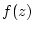

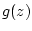

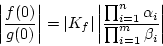
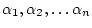 and
and
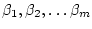 are all the zeros and all the poles of
are all the zeros and all the poles of
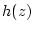 , respectively, that have nonzero magnitude.
, respectively, that have nonzero magnitude.
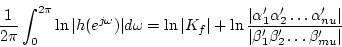
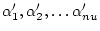 and
and
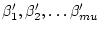 are the zeros and the
poles of
are the zeros and the
poles of