|
You are here :
Control System Design - Index | Book Contents |
Appendix C
| Section C.9
C. Results from Analytic Function Theory
C.9 Application of the Poisson-Jensen Formula to Certain Rational
Functions
Consider the biproper rational function
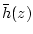 given by
given by
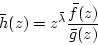 |
(C.9.1) |
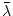 is a integer number, and
is a integer number, and
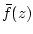 and
and
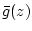 are polynomials of degrees
are polynomials of degrees 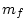 and
and 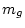 ,
respectively. Then, due to the biproperness of ,
respectively. Then, due to the biproperness of
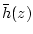 ,
we
have that ,
we
have that
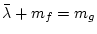 . .
Further assume that
- (i)
-
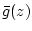 has no zeros outside the open unit disk,
has no zeros outside the open unit disk,
- (ii)
-
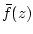 does not vanish on the unit circle, and
does not vanish on the unit circle, and
- (iii)
-
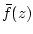 vanishes outside the unit disk at
vanishes outside the unit disk at
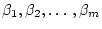 . .
Define
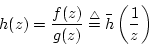 |
(C.9.2) |
where 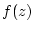 and
and 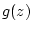 are polynomials.
are polynomials.
Then it follows that
- (i)
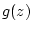 has no zeros in the closed unit disk;
has no zeros in the closed unit disk;
- (ii)
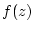 does not vanish on the unit circle;
does not vanish on the unit circle;
- (iii)
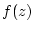 vanishes in the open unit disk at
vanishes in the open unit disk at
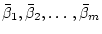 ,
where ,
where
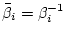 for
for
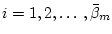 ; ;
- (iv)
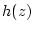 is analytic in the closed unit disk;
is analytic in the closed unit disk;
- (v)
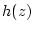 does not vanish on the unit circle;
does not vanish on the unit circle;
- (vi)
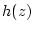 has zeros in the open unit disk, located at
has zeros in the open unit disk, located at
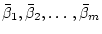 . .
We then have the following result
Lemma C.3
Consider the function 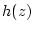 defined in (C.9.2) and
a point defined in (C.9.2) and
a point
 such that such that 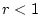 ; then ; then
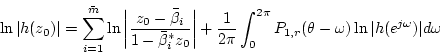 |
(C.9.3) |
where 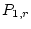 is the Poisson kernel defined in (C.8.18). is the Poisson kernel defined in (C.8.18).
Proof
This follows from a straightforward application of Lemma C.2.

|
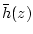 given by
given by
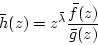
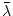 is a integer number, and
is a integer number, and
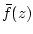 and
and
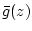 are polynomials of degrees
are polynomials of degrees 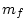 and
and 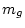 ,
respectively. Then, due to the biproperness of
,
respectively. Then, due to the biproperness of
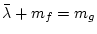 .
.
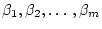 .
.
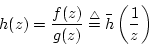
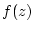 and
and 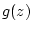 are polynomials.
are polynomials.
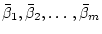 ,
where
,
where
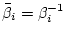 for
for
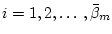 ;
;
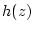 is analytic in the closed unit disk;
is analytic in the closed unit disk;
 such that
such that 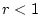 ; then
; then
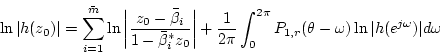
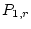 is the Poisson kernel defined in
is the Poisson kernel defined in 