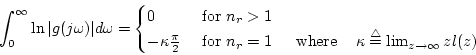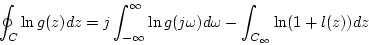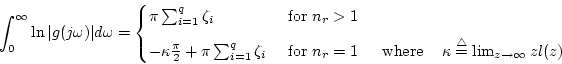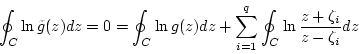|
You are here : Control System Design - Index | Book Contents | Appendix C | Section C.10 C. Results from Analytic Function Theory
We will next review some fundamental results due to Bode.
|
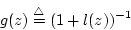 |
(C.10.1) |
and assume that 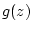 has neither poles nor zeros in the closed RHP. Then
has neither poles nor zeros in the closed RHP. Then
Proof
Because 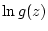 is analytic in the closed RHP,
is analytic in the closed RHP,
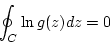 |
(C.10.3) |
where
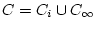 is the contour defined in Figure C.4.
is the contour defined in Figure C.4.
Then
For the first integral on the right-hand side of Equation (C.10.4), we use the conjugate symmetry of 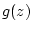 to obtain
to obtain
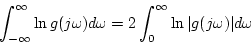 |
(C.10.5) |
For the second integral, we notice that, on 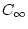 ,
,
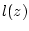 can
be approximated by
can
be approximated by
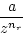 |
(C.10.6) |
The result follows upon using Example C.7 and
noticing that 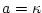 for
for 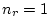 .
.

Remark C.4
If
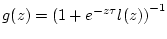 for
for 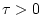 , then result (C.10.9)
becomes
, then result (C.10.9)
becomes
The proof of (C.10.7) follows along the same lines as those of Theorem C.12 and by using the result in Example C.8.
Theorem C.13 (Modified Bode integral)
Let 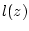 be a proper real, rational function of relative degree
be a proper real, rational function of relative degree
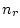 . Define
. Define
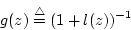 |
(C.10.8) |
Assume that 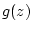 is analytic in the closed RHP and that it has
is analytic in the closed RHP and that it has 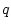 zeros
in the open RHP, located at
zeros
in the open RHP, located at
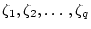 with
with
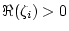 . Then
. Then
Proof
We first notice that 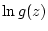 is no longer analytic on the RHP. We
then define
is no longer analytic on the RHP. We
then define
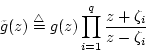 |
(C.10.10) |
Thus,
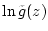 is analytic in the closed RHP. We can then
apply Cauchy's integral in the contour
is analytic in the closed RHP. We can then
apply Cauchy's integral in the contour 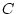 described in Figure C.4 to obtain
described in Figure C.4 to obtain
The first integral on the right-hand side can be expressed as
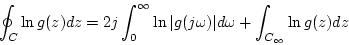 |
(C.10.12) |
where, by using Example C.7.
 |
(C.10.13) |
The second integral on the right-hand side of Equation (C.10.11) can be computed as follows:
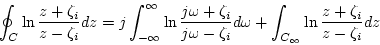 |
(C.10.14) |
We note that the first integral on the right-hand side is zero,
and by using Example C.9, the second integral is equal
to
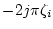 .
Thus, the result follows.
.
Thus, the result follows.

Remark C.5
Note that 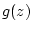 is a real function of
is a real function of 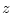 , so
, so
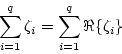 |
(C.10.15) |

Remark C.6
If
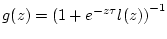 for
for 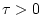 , then the result (C.10.9)
becomes
, then the result (C.10.9)
becomes
The proof of (C.10.16) follows along the same lines as those of Theorem C.13 and by using the result in Example C.8.
Remark C.7
The Poisson, Jensen, and Bode formulae assume that a key function is
analytic, not only inside a domain 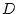 , but also on its border
, but also on its border 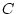 .
Sometimes, there may exist singularities on
.
Sometimes, there may exist singularities on 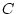 . These can be dealt
with by using an infinitesimal circular indentation in
. These can be dealt
with by using an infinitesimal circular indentation in 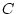 ,
constructed so as to leave
the singularity outside
,
constructed so as to leave
the singularity outside 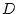 . For the functions of interest to us, the
integral along the indentation vanishes. This is illustrated in
Example C.6 for a logarithmic function, when
. For the functions of interest to us, the
integral along the indentation vanishes. This is illustrated in
Example C.6 for a logarithmic function, when 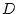 is the
right-half plane and there is a singularity at the origin.
is the
right-half plane and there is a singularity at the origin.