|
You are here : Control System Design - Index | Book Contents | Appendix D | Section D.1 D. Properties of Continuous-Time Riccati Equations
|
![\begin{displaymath}\frac{d\ensuremath{\mathbf{I}} }{dt}=\ensuremath{\mathbf{0}} ...
...\mathbf{M}} (t) \frac{d[\ensuremath{\mathbf{M}} (t)]^{-1}}{dt}
\end{displaymath}](appendixD-img16.png) |
(D.1.5) |
from which we obtain
![\begin{displaymath}\frac{d[\ensuremath{\mathbf{M}} (t)]^{-1}}{dt}=-[\ensuremath{...
...uremath{\mathbf{M}} (t)}{dt}[\ensuremath{\mathbf{M}} (t)]^{-1}
\end{displaymath}](appendixD-img17.png) |
(D.1.6) |
Thus, Equation (D.1.4) can be used with (D.1.2) to yield
which shows that
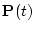 also satisfies
(D.0.1), upon using (D.1.1).
also satisfies
(D.0.1), upon using (D.1.1).
The matrix on the right-hand side of (D.1.2), namely,
is called the Hamiltonian matrix associated with this problem.
Next, note that (D.0.1) can be expressed in compact form as
Then, not surprisingly, solutions to the CTDRE, (D.0.1), are intimately connected to the properties of the Hamiltonian matrix.
We first note that
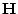 has the following reflexive property:
has the following reflexive property:
where
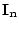 is the identity matrix in
is the identity matrix in
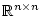 .
.
Recall that a similarity transformation preserves the eigenvalues;
thus, the eigenvalues of
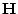 are the same as those of
are the same as those of
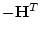 .
On the other hand, the eigenvalues of
.
On the other hand, the eigenvalues of
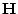 and
and
 must be the same. Hence, the spectral set of
must be the same. Hence, the spectral set of
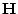 is
the union of two sets,
is
the union of two sets, 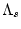 and
and 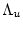 ,
such that, if
,
such that, if
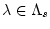 ,
then
,
then
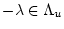 .
We assume that
.
We assume that
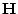 does not contain any eigenvalue on the imaginary axis
(note that it suffices, for this to occur, that
does not contain any eigenvalue on the imaginary axis
(note that it suffices, for this to occur, that
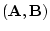 be stabilizable and that the pair
be stabilizable and that the pair
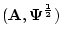 have no undetectable poles on
the stability boundary). In this case,
have no undetectable poles on
the stability boundary). In this case, 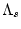 can be so
formed that it contains only the eigenvalues of
can be so
formed that it contains only the eigenvalues of
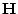 that lie
in the open LHP. Then, there always exists a nonsingular
transformation
that lie
in the open LHP. Then, there always exists a nonsingular
transformation
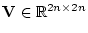 such that
such that
where
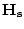 and
and
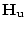 are diagonal matrices with
eigenvalue sets
are diagonal matrices with
eigenvalue sets 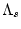 and
and 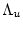 ,
respectively.
,
respectively.
We can use
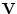 to transform the matrices
to transform the matrices
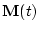 and
and
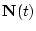 ,
to obtain
,
to obtain
Thus, (D.1.2) can be expressed in the equivalent form:
If we partition
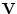 in a form consistent with the matrix Equation (D.1.13), we have that
in a form consistent with the matrix Equation (D.1.13), we have that
The solution to the CTDRE is then given by the following lemma.
Lemma D.2 A solution for Equation (D.0.1) is given by
where
Proof
From (D.1.12), we have
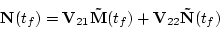 |
Hence, from (D.1.3),
or
or
Now, from (D.1.10),
![\begin{displaymath}=\left[ \ensuremath{\mathbf{V}} _{21}\ensuremath{\mathbf{\til...
...12}\ensuremath{\mathbf{\tilde{N}}} (t)\right] ^{-1} \nonumber
\end{displaymath}](appendixD-img52.png) |
![\begin{displaymath}=\left[ \ensuremath{\mathbf{V}} _{21}+\ensuremath{\mathbf{V}}...
...nsuremath{\mathbf{\tilde{M}}} (t)]^{-1}\right] ^{-1} \nonumber
\end{displaymath}](appendixD-img53.png) |
and the solution to (D.1.13) is
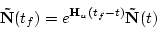 |
Hence,
Substituting (D.1.25) into (D.1.23) gives the result.

![\begin{displaymath}
\ensuremath{\mathbf{P}} (t)=\ensuremath{\mathbf{N}} (t)[\ensuremath{\mathbf{M}} (t)]^{-1}
\end{displaymath}](appendixD-img8.png)
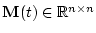 and
and
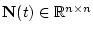 satisfy the following equation:
satisfy the following equation:
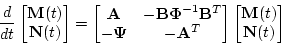
![\begin{displaymath}
\ensuremath{\mathbf{N}} (t_f)[\ensuremath{\mathbf{M}} (t_f)]^{-1}=\ensuremath{\boldsymbol{\Psi}} _f
\end{displaymath}](appendixD-img12.png)
![\begin{displaymath}
\frac{d\ensuremath{\mathbf{P}} (t)}{dt}=\frac{d\ensuremath{...
...\mathbf{N}} (t)\frac{d[\ensuremath{\mathbf{M}} (t)]^{-1}}{dt}
\end{displaymath}](appendixD-img13.png)
![$[\ensuremath{\mathbf{M}} (t)]^{-1}$](appendixD-img14.png) can be computed by noting
that
can be computed by noting
that
![$\ensuremath{\mathbf{M}} (t)[\ensuremath{\mathbf{M}} (t)]^{-1}=\ensuremath{\mathbf{I}} $](appendixD-img15.png) ;
then
;
then
![\begin{displaymath}
\begin{split}
- \frac{d\ensuremath{\mathbf{P}} (t)}{dt}&=\e...
...h{\mathbf{N}} (t)[\ensuremath{\mathbf{M}} (t)]^{-1}
\end{split}\end{displaymath}](appendixD-img18.png)
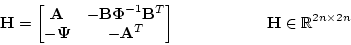
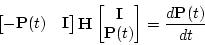
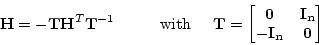
![\begin{displaymath}[\ensuremath{\mathbf{V}} ]^{-1} \ensuremath{\mathbf{H}}\ensur...
...nsuremath{\mathbf{0}} & \ensuremath{\mathbf{H_u}} \end{bmatrix}\end{displaymath}](appendixD-img34.png)
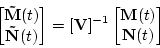


![\begin{displaymath}
\ensuremath{\mathbf{P}} (t)= \ensuremath{\mathbf{P_1}} (t) [\ensuremath{\mathbf{P_2}} (t)]^{-1}
\end{displaymath}](appendixD-img43.png)

![\begin{displaymath}
\ensuremath{\mathbf{P_2}} (t)=\bigl[\ensuremath{\mathbf{V_{...
...mathbf{V_a}} e^{\ensuremath{\mathbf{H_s}} (t_f-t)}\bigr]^{-1}
\end{displaymath}](appendixD-img45.png)
![\begin{displaymath}
\ensuremath{\mathbf{V_a}}\stackrel{\rm\triangle}{=}-[\ensure...
...(t_f)\left[\ensuremath{\mathbf{\tilde{M}}} (t_f) \right]^{-1}
\end{displaymath}](appendixD-img46.png)
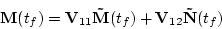
![\begin{displaymath}\left[
\ensuremath{\mathbf{V}} _{21}\ensuremath{\mathbf{\til...
...lde{N}}} (t_f)\right]
^{-1}
=\ensuremath{\boldsymbol{\Psi}} _f
\end{displaymath}](appendixD-img49.png)
![\begin{displaymath}\left[
\ensuremath{\mathbf{V}} _{21}+\ensuremath{\mathbf{V}}...
...}} (t_f)]^{-1}\right]
^{-1}=\ensuremath{\boldsymbol{\Psi}} _f
\end{displaymath}](appendixD-img50.png)
![\begin{displaymath}\ensuremath{\mathbf{\tilde{N}}} (t_f)[\ensuremath{\mathbf{\ti...
...\ensuremath{\mathbf{V}} _{11}\right] =\ensuremath{\mathbf{V_a}}\end{displaymath}](appendixD-img51.png)
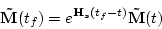
![\begin{displaymath}\ensuremath{\mathbf{\tilde{N}}} (t)[\ensuremath{\mathbf{\tild...
...f{\tilde{M}}} (t_f)]^{-1}e^{\ensuremath{\mathbf{H}} _s(t_f-t)}
\end{displaymath}](appendixD-img56.png)