|
You are here :
Control System Design - Index | Book Contents |
Appendix B
| Section B.5
B. Smith McMillan Forms
B.5 Poles and Zeros
The Smith-McMillan form can be utilized to give an unequivocal
definition of poles and zeros in the multivariable case. In
particular, we have:
Definition B.11
Consider a transfer-function matrix ,
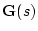 . .
| (i) |
|
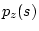 and
and 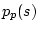 are said to be the zero
polynomial and the pole polynomial of
are said to be the zero
polynomial and the pole polynomial of
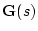 ,
respectively, where ,
respectively, where
 |
(B.5.1) |
and where
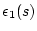 , ,
 , ,
 , ,
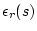 and
and
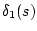 , ,
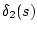 , ,
 , ,
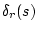 are the polynomials in the Smith-McMillan form,
are the polynomials in the Smith-McMillan form,
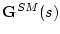 of
of
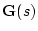 . .
Note that 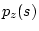 and
and 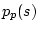 are monic polynomials.
are monic polynomials.
|
| (ii) |
|
The zeros of the matrix
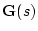 are
defined to be the roots of
are
defined to be the roots of 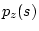 ,
and the poles of ,
and the poles of
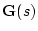 are defined to be the roots of
are defined to be the roots of 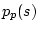 . .
|
| (iii) |
|
The McMillan degree of
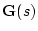 is defined as the degree of
is defined as the degree of 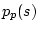 . .
|
In the case of square plants (same number of inputs as outputs),
it follows that
![$ \det[\mathbf{G}(s)]$](appendixb-img82.png) is a simple function of
is a simple function of
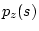 and
and 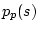 .
Specifically, we have .
Specifically, we have
![\begin{displaymath}\det[\mathbf{G}(s)]=K_\infty \frac{p_z(s)}{p_p(s)}
\end{displaymath}](appendixb-img83.png) |
(B.5.2) |
Note, however, that 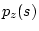 and
and 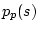 are not necessarily
coprime. Hence, the scalar rational function
are not necessarily
coprime. Hence, the scalar rational function
![$ \det[\mathbf{G}(s)]$](appendixb-img82.png) is not sufficient to determine all zeros and poles of is not sufficient to determine all zeros and poles of
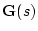 .
However, the relative degree of .
However, the relative degree of
![$ \det[\mathbf{G}(s)]$](appendixb-img82.png) is equal to the difference between the
number of poles and the number of zeros of the MIMO
transfer-function matrix.
is equal to the difference between the
number of poles and the number of zeros of the MIMO
transfer-function matrix.
|
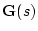 .
.
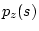 and
and 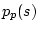 are said to be the zero
polynomial and the pole polynomial of
are said to be the zero
polynomial and the pole polynomial of

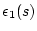 ,
,
 ,
,
 ,
,
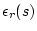 and
and
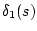 ,
,
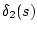 ,
,
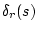 are the polynomials in the Smith-McMillan form,
are the polynomials in the Smith-McMillan form,
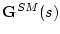 of
of
![$ \det[\mathbf{G}(s)]$](appendixb-img82.png) is a simple function of
is a simple function of
![\begin{displaymath}\det[\mathbf{G}(s)]=K_\infty \frac{p_z(s)}{p_p(s)}
\end{displaymath}](appendixb-img83.png)