You are here : Control System Design - Index | Book Contents | Chapter 2 | Section 2.3

2. Introduction to the Principles of Feedback


2.3.2 Modeling

To make progress on the control-system design problem as set out above, it is first necessary to gain an understanding of how the process operates. This understanding is typically expressed in the form of a mathematical model that describes the steady-state and the dynamic behavior of the process. To construct such a model, we first define relevant process variables. Thus, we introduce the following:


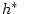$h^{*}\quad $: commanded level of steel in mould
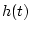$h(t)\quad $: actual level of steel in mould
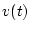$v(t)\quad $: valve position
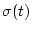$\sigma(t)\quad $: casting speed
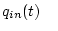$q_{in}(t)\quad $: inflow of matter into the mould
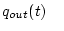$q_{out}(t)\quad $: outflow of matter from the mould.


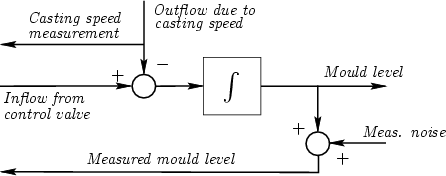
Physics suggests that the mould level will be proportional to the integral of the difference between in- and outflow:


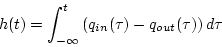\begin{displaymath}h(t)=\int_{-\infty}^t \left( q_{in}(\tau)-q_{out}(\tau)\right) d\tau \end{displaymath} (2.3.1)

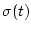where we have assumed a unit cross-section of the mould for simplicity. We also assume, again for simplicity, that the measurements of valve position, v(t) and casting speed, $\sigma(t)$, are calibrated such that they actually indicate the corresponding in- and outflows:


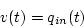\begin{displaymath}v(t)=q_{in}(t) \end{displaymath} (2.3.2)


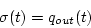\begin{displaymath}\sigma(t)=q_{out}(t) \end{displaymath} (2.3.3)

Hence, the process model becomes


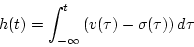\begin{displaymath}h(t)=\int_{-\infty}^t\left(v(\tau)-\sigma(\tau)\right)d\tau \end{displaymath} (2.3.4)

The casting speed can be measured fairly accurately, but mould-level sensors are typically prone to high-frequency measurement noise, which we take into account by introducing an additive spurious signal n(t):


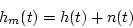\begin{displaymath}h_m(t)=h(t)+n(t) \end{displaymath} (2.3.5)

where hm(t) is the measurement of h(t) corrupted by noise. A block diagram of the overall process model and the measurements is shown in Figure 2.3.


Figure 2.3: Block diagram of the simplified mould-level dynamics, sensors, and actuator
Block diagram of the simplified mould-level dynamics, sensors, and actuator

This is a very simple model, but it captures the essence of the problem.