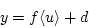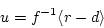|
You are here : Control System Design - Index | Book Contents | Chapter 2 | Section 2.5 2. Introduction to the Principles of Feedback
|
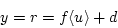 |
(2.5.2) |
from which we could derive a control law, by solving for u. This leads to
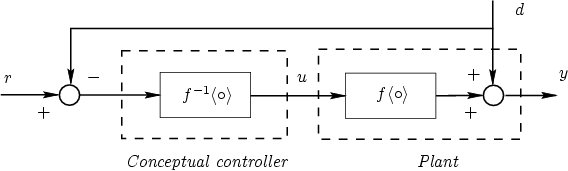
This idea is illustrated in Figure 2.6.
This is a conceptual solution to the problem. However, a little thought indicates that the answer given in (2.5.3) presupposes certain stringent requirements for its success. For example, inspection of equations (2.5.1) and (2.5.3) suggests the following requirements:
Of course, these are very demanding requirements. Thus, a significant part of Automatic Control theory deals with the issue of how to change the control architecture so that inversion is achieved but in a more robust fashion and so that the stringent requirements set out above can be relaxed.
To illustrate the meaning of these requirements in practice, we briefly review a number of situations.
Example 2.1 (Heat exchanger) Consider the problem of a heat exchanger in which water is to be heated by steam having a fixed temperature. The plant output is the water temperature at the exchanger output and the manipulated variable is the air pressure (3 to 15 [psig]) driving a pneumatic valve that regulates the amount of steam feeding the exchanger.
In the solution of the associated control problem, the following issues should be considered:
- Pure time delays might be a significant factor, because this plant involves mass and energy transportation. However a little thought indicates that a pure time delay does not have a realizable inverse (otherwise we could predict the future), and hence R3 will not be met.
- It can easily happen that, for a given reference input, the control law (2.5.3) leads to a manipulated variable outside the allowable input range (3 to 15 [psig] in this example). This will lead to saturation in the plant input. Condition R5 will then not be met.

Example 2.2 (Flotation in mineral processing) In copper processing, one crucial stage is the flotation process. In this process, the mineral pulp (water and ground mineral) is continuously fed to a set of agitated containers where chemicals are added to separate (by flotation) the particles with high copper concentration. From a control point of view, the goal is to determine the appropriate addition of chemicals and the level of agitation to achieve maximal separation.
Characteristics of this problem are as follows:
- The process is complex (physically distributed, time varying, highly nonlinear, multivariable, and so on) and hence it is difficult to obtain an accurate model for it. Thus, R1 is hard to satisfy.
- One of the most significant disturbances in this process is the size of the mineral particles in the pulp. This disturbance is actually the output of a previous stage (grinding). To apply a control law derived from (2.5.3), one would need to measure the size of all these particles or (at least) to obtain some average measure of this. Thus, condition R4 is hard to satisfy.
- Pure time delays are also present in this process, and thus condition R3 cannot be satisfied.

One could imagine various other practical cases where one or more of the requirements listed above cannot be satisfied. Thus, the only sensible way to proceed is to accept that there will inevitably be intrinsic limitations and to pursue the solution within those limitations. With this in mind, we will impose constraints that will allow us to solve the problem subject to the limitations that the physical set-up imposes. The most commonly used constraints are as follows:
| L1 | to restrict attention to those problems where the prescribed behavior (reference signals) belong to restricted classes and where the desired behavior is achieved only asymptotically; | |
| L2 | To seek approximate inverses. |
In summary, we can conclude the following:
| In principle, all controllers implicitly generate an inverse of the process, in sofar as this is feasible. Controllers differ with respect to the mechanism used to generate the required approximate inverse. |
1 We introduce this term here loosely. A more rigorous treatment will be deferred to Chapter 19.
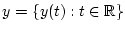 .
.
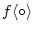 ,
to denote an
operator mapping
,
to denote an
operator mapping 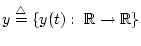 .
An
operator,
.
An
operator,
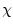 ,
onto
,
onto