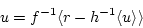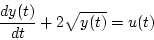You are here : Control System Design - Index | Book Contents | Chapter 2 | Section 2.6

2. Introduction to the Principles of Feedback

 
2.6 High-Gain Feedback and Inversion

As we will see later, typical models used to describe real plants cannot be inverted exactly. We will next show, however, that there is a rather intriguing property of feedback that implicitly generates an approximate inverse of dynamic transformations, without the inversions having to be carried out explicitly.

To develop this idea, let us replace the conceptual controller shown in Figure 2.6 by the realization shown in Figure 2.7. As before, f represents the process model. The transformation h will be described further below.


Figure 2.7: Realization of conceptual controller
Realization of conceptual controller

As in section §2.5, r, u, y can be interpreted as real numbers, and $h\langle\circ\rangle$, $f\langle \circ \rangle$ are scalar linear gains, on a first reading. On a second reading, these can be given the general nonlinear interpretation introduced in section §2.5.

From Figure 2.7, we see that


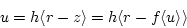\begin{displaymath}u=h\langle r-z\rangle=h\langle r-f\langle u\rangle\rangle \end{displaymath} (2.6.1)

Thus,


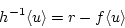\begin{displaymath}h^{-1}\langle u\rangle =r-f\langle u\rangle \end{displaymath} (2.6.2)

from which we finally obtain


\begin{displaymath}u=f^{-1}\langle r-h^{-1}\langle u\rangle\rangle \end{displaymath} (2.6.3)

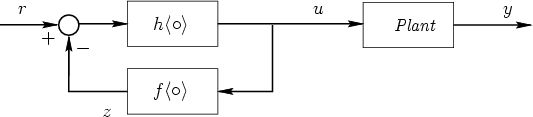
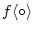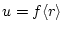Equation (2.6.3) suggests that the loop in Figure 2.7 implements an approximate inverse of $f\langle \circ \rangle$, that is, $u=f\langle r\rangle$, if


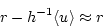\begin{displaymath}r-h^{-1}\langle u\rangle \approx r \end{displaymath} (2.6.4)

We see that this is achieved if h-1 is small, that is, if h is a high-gain transformation.

Hence, if f characterizes our knowledge of the plant and if h is a high-gain transformation, then the architecture illustrated in Figure 2.7 effectively builds an approximate inverse for the plant model without requiring that the model of the plant, f be explicitly inverted. We illustrate this idea by an example.

Example 2.3 Assume that a plant can be described by the model

\begin{displaymath}\frac{dy(t)}{dt}+2\sqrt{y(t)}=u(t) \end{displaymath} (2.6.5)

and that a control law is required to ensure that y(t) follows a slowly varying reference.

One way to solve this problem is to construct an inverse for the model that is valid in the low-frequency region. Using the architecture in Figure fig:inv1, we obtain an approximate inverse, provided that 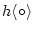$h\langle\circ\rangle$ has large gain in the low-frequency region. A simple solution is to choose 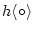$h\langle\circ\rangle$ to be an integrator that has infinite gain at zero frequency. 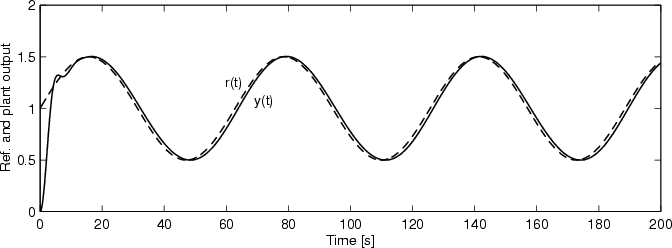The output of the controller is then fed to the plant. The result is illustrated in Figure 2.8, which shows the reference and the plant outputs. The reader might wish to explore this example further by using the SIMULINK file tank1.mdl on the accompanying CD.

$\Box \Box \Box $


Figure 2.8: Tank level control by using approximate inversion
Tank level control by using approximate inversion