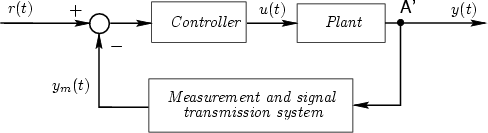
You are here : Control System Design - Index | Book Contents | Chapter 2 | Section 2.9

2. Introduction to the Principles of Feedback

2.9 Measurements

We have seen that one of the key issues in feedback control is that there must exist suitable measurements to feed back. Indeed, if one can measure a variable, then there is a good chance that one can design a controller to bring it to a desired reference value.

A more accurate description of the feedback control loop, including sensors, is shown in Figure 2.11. From this figure, it can be seen that what we actually control is the measured value rather than the true output. These can be quite different.


Figure 2.11: Closed-loop control with sensors
Closed-loop control with sensors

Hence the measurement system should ideally satisfy requirements such as the following:

  • Reliability. It should operate within the necessary range.

  • Accuracy. For a variable with a constant value, the measurement should settle to the correct value.

  • Responsiveness. If the variable changes, the measurement should be able to follow the changes. Slow responding measurements can not only affect the quality of control but can actually make the feedback loop unstable. Loop instability can arise even though the loop has been designed to be stable for exact measurement of the process variable.

  • Noise immunity. The measurement system, including the transmission path, should not be significantly affected by exogenous signals, such as measurement noise.

  • Linearity. If the measurement system is not linear, then at least the nonlinearity should be known, so that it can be compensated for.

  • Nonintrusive measurement. The measuring device should not significantly affect the behavior of the plant.

In most of the sequel, we will assume that the measurement system is sufficiently good, so that only measurement noise needs to be accounted for. This ideal measurement loop will be known as a unity feedback loop .