|
You are here : Control System Design - Index | Book Contents | Appendix D | Section D.4 D. Properties of Continuous-Time Riccati EquationsD.4 Convergence of Solutions of the CTARE to the Stabilizing Solution of the CTAREFinally, we show that, under reasonable conditions, the solution of the CTDRE will converge to the unique stabilizing solution of the CTARE. In the sequel, we will be particularly interested in the stabilizing solution to the CTARE.
Lemma D.5
Provided that
Proof
We observe that the eigenvalues of
given that
The result then follows from (D.1.16) to (D.1.17).
Remark D.1
Actually, provided that
|
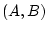 is stabilizable and that
is stabilizable and that
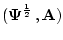 has no unobservable poles on the
imaginary axis and that
has no unobservable poles on the
imaginary axis and that
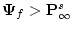 , then
, then
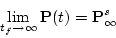
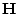 can be grouped so that
can be grouped so that
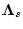 contains only eigenvalues that lie in the left-half
plane. We then have that
contains only eigenvalues that lie in the left-half
plane. We then have that
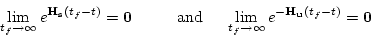
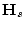 and
and
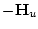 are matrices with
eigenvalues strictly inside the LHP.
are matrices with
eigenvalues strictly inside the LHP.
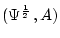 is detectable, then it
suffices to have
is detectable, then it
suffices to have
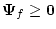 in
in 